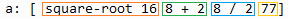Evaluation
There is a good description of Rebol's evaluation here. It's pretty much the same for Red. I'll not repeat that explanation, instead, I'll describe how I see Red's evaluation from my personal point of view. Again, this may prove inaccurate, but so far it explains Red's behavior pretty well.
Red, the furious evaluator
Once triggered, Red will start reading a text from left to right (→) executing all operations it can find. If it recognizes an operation that requires arguments, it picks the arguments from this main text as needed to come to a final value. Take a look at the concept of evaluable groups and argument picking. Red considers text (strings) as a block of characters, so this main text of Red code is just a big block for Red, even without brackets or quotes.
What triggers Red's fury?
Red is triggered by the "command" do. You don't always have to actually type do, when you run a script or press enter at the console, what is happening is that you are applying an implicit do to the text ahead. In the case of a script, the evaluation only begins after the interpreter finds the characters "Red ["
An interesting consequence of all this is that, although it's not generally considered good practice, you can actually execute text:
>> do "3 + 5"
== 8
>> 3 + 5 ;same thing. The "do" is implicit and input is text (but not a string! datatype).
== 8
If it's an evaluation, what is the result?
The result of a Red interpretation is the resulting value of the last evaluable group. Of course you can do all sorts of interesting things along the way, as writing files, reading web pages and creating beautiful drawings on your screen, but the value returned by Red (if there is one) is this last result.
>> do "3 + 5 7 * 8 print 69"
69
What halts Red's fury?
The end of the text (code) and comments, of course.
But also, Red's evaluation skips blocks inside the main text (blocks within the main block), just leaves them as they are. It only evaluates them if they are an argument of an operation, noting that this operation may be another do:
>> do {print "hello" 7 + 9 [8 + 2]} ; the last result is the unevaluated block
hello
== [8 + 2]
>> do {print "hello" 7 + 9 print [8 + 2]}
hello
10
>> do {print "hello" 7 + 9 do[8 + 2]}
hello
== 10
You will find out that, to develop Red scripts, sometimes you need the resulting values of all evaluable groups in a block, not just the last one. You can achieve that with reduce. It returns a block with all the results. However, It' not as if you applied a do to each evaluable group inside the block, as you can see here:
>> reduce [3 + 5 7 * 8 print 69]
69
== [8 56 unset]
>> reduce [3 + 5 7 * 8 "print 69"] ; do "print 69" should print 69!
== [8 56 "print 69"]
Math evaluation order
I'm still looking for a simple rule to explain Red's math evaluation sequence. For the moment, I have two favorite candidates. The first is very straightforward and easy to use. The second is not very practical, but gives a view of how (I think) the Red interpreter "thinks", and so I believe it is a good idea to take a look at it to grasp some concepts that may be useful.
1) My favorite rule for the moment:
1- All operations with infix operators that have only values (not functions) as operands are evaluated first. If these infix expressions have more than two operands they are evaluated from left to right ( → ) with no precedence (i.e., multiplication doesn't automatically get computed before addition) .
2- Then the whole expression is evaluated from right to left (← ).
>> square-root 2 + 2 + square-root 3 * 3 * square-root 1 + 4 * 5
== 3.272339214155429

2) My second favorite, the 3 concepts explanation:
This seems to work and I think that's somehow what the interpreter does.
It's not a simple rule and I think it may not be formally accurate, as I'm not sure that every infix operator has an exact correspondent function operation.
Concept 1: Left to right always →
In Red, things are evaluated from left to right. There is no "order of precedence" as in other languages (i.e., multiplication doesn't automatically get computed before addition). However, you may enclose the functions in parentheses to force precedence.
>> 2 + 3 * 5
== 25 ; not 17!
Not only expressions, but the whole code of a program is evaluated from left to right.
Infix operators
"+", "-", "*", "/" are called infix operators. They correspond to the functions add , multiply, divide and subtract, which need two arguments. So:
3 + 2 is the same as add 3 2
5 * 8 is the same as multiply 5 8 ...
...and so on.
2 + 3 * 5 is just a more readable form of multiply add 2 3 5 . Red's interpreter does the conversion for you.
Concept 2: Evaluable groups.
When you have a chunk of code, there are groups of words that are evaluable, that is, can be reduced to basic datatypes. For example [square-root 16 8 + 2 8 / 2 77] is actually made of 4 evaluable groups: square-root 16 ; 8 + 2 ; 8 / 2 and 77. You can use reduce to "see" the values of evaluable groups:
>> a: [ square-root 16 8 + 2 8 / 2 77]
>> reduce a
== [4.0 10 4 77]
Concept 3: Functions pick their arguments from the evaluable groups
A function takes its arguments from the evaluable groups ahead of it, from left to right (think of infix operators as syntax sugar for their function counterparts). A function that needs 1 argument, take the next evaluable group; a function that needs 2 arguments, take the next 2 evaluable groups, and so on. Notice that a function may use an evaluable group that has another function in it. In this case, it holds its evaluation until the argument function is evaluated, and then use the result.
Again, no precedence rules, just left to right.
A consequence of that is that an expression like this...
square-root 16 + square-root 16
...is not 8, as many would expect, but 4.47213595499958, because what Red sees is:

( or even: square-root add 16 square-root 16)
That is: One function that has one argument and one evaluable group (which happens to have a function in it).
To obtain that intuitive 8, one must use parentheses:
>> (square-root 16) + square-root 16
== 8.0
Another example, mixing an infix operator and its corresponding function:
>> reduce [add 8 + 2 * 3 8 / 2 divide 16 / 2 2 * 2]
== [34 2]

Other explanations:
These are some other "rules" I have seen discussed:
#1
"Left-to-right and operators take precedence over functions and if an infix operator sees a function as its second operand, evaluates it"
#2
"In general, expressions are evaluated from left to right; however, within each expression evaluation occurs from right to left".
#3
"Each expression takes as many arguments as it should, each argument in turn may be another expression and Red will parse the expressions until they all have a full set of arguments".